 Sirius A et Sirius B
Sirius A et Sirius B
Difficulté : ☆☆
Temps : 30 min

La figure trace le mouvement vrai de la composante Sirius B par rapport à Sirius A dans le plan orbital.
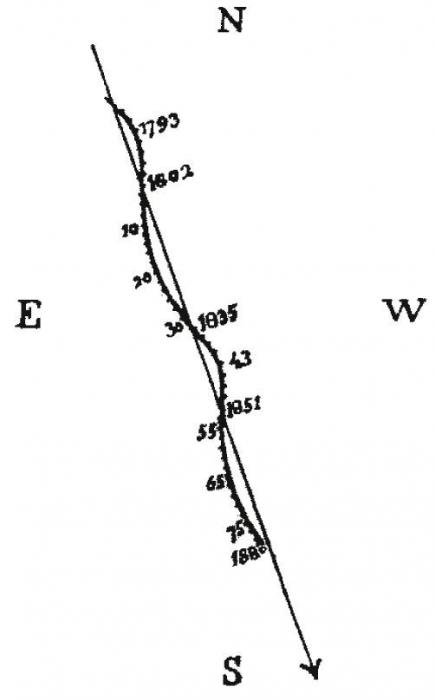
Mouvement de Sirius dans le plan du ciel, reporté par Camille Flammarion au XIXe siècle.
Crédit :
ASM
Question 1)
Etalonner la figure de l'appliquette, en tenant compte du fait que les portions de cercle centrés sur Sirius A sont espacés de 1 seconde d'angle, et définir le rapport d'unité permettant de lire directement des secondes d'angle sur la figure.
Activité soit l'outil 'ligne', soit l'outil 'cercle'.
Faire une règle de trois et définir le rapport d'unité.
Question 2)
Estimer le demi-grand axe de l'orbite relative et la période.
Pour le demi-grand axe : repérer les projections des péri- et apoastre.
Pour la période : s'appuyer sur les valeurs au voisinage de l'apoastre.
Question 3)
La parallaxe du système vaut 0.379". En déduire la somme des masses des deux composantes (en unités de masse solaire).
Traduire la parallaxe en distance.
De la valeur angulaire du demi-grand axe et de la distance, déterminer le demi-grand axe en UA.
Utiliser la 3ème loi de Kepler
Question 4)
Le mouvement de Sirius A par rapport au barycentre présente une demi-amplitude de 2.35" au cours d'une orbite (corrigée de la projection du plan orbital sur le plan du ciel). Comparer cette amplitude au mouvement relatif des 2 composantes, et en déduire la masse de chaque composante.
La demi-amplitude est à comparer au demi-grand axe.
- Question 1
Aide :
Activité soit l'outil 'ligne', soit l'outil 'cercle'.
Aide :
Faire une règle de trois et définir le rapport d'unité.
Solution :
Avec l'outil 'cercle' centré sur Sirius A, 10" correspondent à 350 unités. On définit le rapport d'unité : 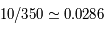
- Question 2
Aide :
Pour le demi-grand axe : repérer les projections des péri- et apoastre.
Aide :
Pour la période : s'appuyer sur les valeurs au voisinage de l'apoastre.
Solution :
D'après la figure, on déduit la période 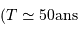 et le demi-grand axe de l'orbite relative
et le demi-grand axe de l'orbite relative 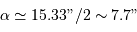
- Question 3
Aide :
Traduire la parallaxe en distance.
Aide :
De la valeur angulaire du demi-grand axe et de la distance, déterminer le demi-grand axe en UA.
Aide :
Utiliser la 3ème loi de Kepler
Solution :
Si 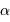 est le demi-grand axe mesuré en secondes d'arc et
est le demi-grand axe mesuré en secondes d'arc et 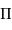 la parallaxe, le demi-grand axe linéaire
la parallaxe, le demi-grand axe linéaire 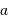 , mesuré en UA est alors égal à
, mesuré en UA est alors égal à 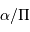 , soit
, soit 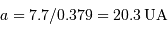 .
.
D'après la troisième loi de Kepler, on a par ailleurs :
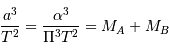
où 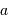 est exprimé en UA,
est exprimé en UA, 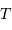 en années, et
en années, et 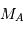 et
et 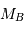 en masse solaire. Ce qui donne :
en masse solaire. Ce qui donne :
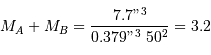
- Question 4
Aide :
Définir le barycentre.
Aide :
La demi-amplitude est à comparer au demi-grand axe.
Solution :
La définition du barycentre G donne :
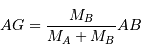
On peut ainsi comparer la demi-amplitude de AG au demi-grand axe, pour obtenir le rapport 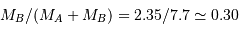 .
.
On en déduit les masses respectives : 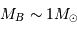 et
et 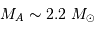 .
.
 Sirius A et Sirius B
Sirius A et Sirius B

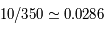
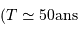 et le demi-grand axe de l'orbite relative
et le demi-grand axe de l'orbite relative 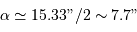
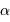 est le demi-grand axe mesuré en secondes d'arc et
est le demi-grand axe mesuré en secondes d'arc et 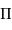 la parallaxe, le demi-grand axe linéaire
la parallaxe, le demi-grand axe linéaire 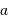 , mesuré en UA est alors égal à
, mesuré en UA est alors égal à 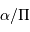 , soit
, soit 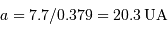 .
.
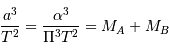
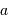 est exprimé en UA,
est exprimé en UA, 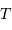 en années, et
en années, et 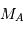 et
et 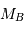 en masse solaire. Ce qui donne :
en masse solaire. Ce qui donne :
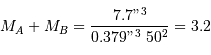
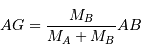
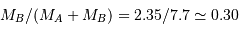 .
.
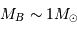 et
et 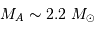 .
.