
 Trigonométrie sphérique
Trigonométrie sphérique
Difficulté : ☆
Temps : 30 min
Un peu de trigonométrie sphérique nous apprend que la distance angulaire entre 2 objets A et B de coordonnées équatoriales respectives 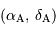 et
et 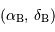 s'écrit :
s'écrit :
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation10.png)
Question 1)
Vérifier cette expression dans le cas particulier où A et B sont 2 objets sur l'équateur céleste.
AideAideAideSolution
[1 points]
Dans ce cas, les déclinaisons sont nulles toutes les deux.
Un peu de trigonométrie : 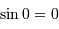 et
et 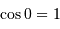 .
.
Un peu plus de trigonométrie : comme 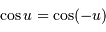 ,
, 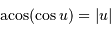 .
.
Les déclinaisons de A et B étant toutes deux nulles, la relation se réécrit simplement :
![d = {\mathrm{acos}} \left[\cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation15.png)
D'où la solution, évidemment simple :
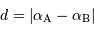
Question 2)
Vérifier cette expression dans le cas particulier où A et B ont même ascension droite.
AideSolution
[2 points]
Peut-être est-il utile de rappeler que 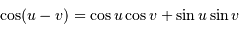
Avec des ascensions droites égales, la distance angulaire se réécrit :
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \right]](../pages_reperes/equations_referentiel/equation18.png)
Plus simplement :
![d = {\mathrm{acos}} \left[ \cos( \delta _{\mathrm{A}} - \delta _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation19.png)
Soit
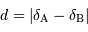
Là encore, le résultat est assez intuitif
Question 3)
Vérifier cette expression dans le cas particulier où A et B sont séparés de 12 h en ascension droite. Préciser le résultat lorsque, en plus, les déclinaisons sont égales.
AideAideAideSolution
[3 points]
Que devient dans ce cas la contribution du terme avec les ascensions droites ?
Encore un peu de trigonométrie :
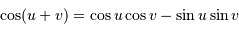
Moins courant, mais un cercle trigonométrique le justifie aisément :
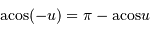
La solution
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation23.png)
s'écrit dans ce cas, avec 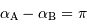 .
.
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} - \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \right] = \pi - {\mathrm{acos}} \left[ \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} - \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} \right]](../pages_reperes/equations_referentiel/equation25.png)
Et donc, dans ce cas :
![d = \pi - {\mathrm{acos}} [ \cos ( \delta _{\mathrm{A}} + \delta _{\mathrm{B}}) ] = \pi - | \delta _{\mathrm{A}} + \delta _{\mathrm{B}}|](../pages_reperes/equations_referentiel/equation26.png)
Si, de plus, les déclinaisons sont égales, on trouve alors
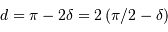
La distance angulaire, en passant par les pôles, est bien égale à 2 fois la colatitude ; la colatitude est le complément à 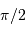 (ou 90 deg) de la latitude.
(ou 90 deg) de la latitude.

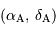 et
et 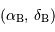 s'écrit :
s'écrit :
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation10.png)