Apprendre

Les forces de marée sont des forces différentielles

La Terre n'est pas un point, mais a une dimension finie. Or l'intensité du champ gravitationnel de la Lune varie comme l'inverse du carré de la distance à la Lune. Il en résulte une attraction différentielle qui déforme la Terre. On peut estimer la valeur du champ de marée 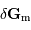$\delta \mathbf{G} _{\mathrm{m}}$ dans le cadre du modèle de l'océan global. On démontre que le module de 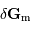$\delta \mathbf{G} _{\mathrm{m}}$ est de l'ordre de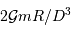 ${2{\cal G}mR/D^{3}}$

Démonstration

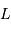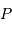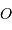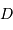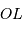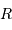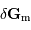Calcul du champ de marée. On estime la marée créée par la Lune en un point courant du globe terrestre, que l'on repère par rapport au centre de la Terre. On note {D} la distance , et le rayon terrestre. La composante du champ de marée $\delta \mathbf{G} _{\mathrm{m}}$ en 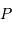représente la différence du champ lunaire entre les points 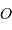et 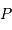. 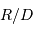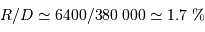Les calculs sont menés au 1er ordre par rapport au petit terme R/D (car $R/D \simeq 6400/380\ 000 \simeq 1.7\ \%$ ) :

$\begin{eqnarray*} \delta \mathbf{G} _{\mathrm{m}} &=& {{\cal G} m} { {\mathbf{PL}} \over PL^{3}} - {{\cal G} m} { {\mathbf{OL}} \over OL^{3}} \\ &=& {{\cal G} m} \left[{ {\mathbf{PO}}+ {\mathbf{OL}} \over PL^{3}} - { {\mathbf{OL}} \over OL^{3}} \right]\\ &\simeq& {{\cal G} m} \left[ { {\mathbf{PO}} \over {D}^{3}} + { {\mathbf{OL}} \over PL^{3}} - { {\mathbf{OL}} \over {D}^{3}} \right]\\ \end{eqnarray*}$

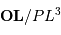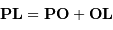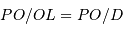On estime alors le terme ${\mathbf{OL}} / PL^{3}$ de l'équation précédente, en injectant la relation de Chasles ${\mathbf{PL}} = {\mathbf{PO}} + {\mathbf{OL}}$ , et toujours au premier ordre en PO / OL = PO / {D} :

$\begin{eqnarray*} { {\mathbf{OL}} \over PL^{3}}&=& { {\mathbf{OL}} \over [{ {\mathbf{PL}}^{2}}]^{3/2}}= { {\mathbf{OL}} \over [( {\mathbf{PO}}+ {\mathbf{OL}})^{2}]^{3/2}}\\ \\ &\simeq& { {\mathbf{OL}} \over {D}^{3} \left( 1 + 2\ {\mathbf{PO}} . {\mathbf{OL}} / {D}^{2} \right)^{3/2}}\\ &\simeq& { {\mathbf{OL}} \over {D}^{3}} \left(1 - 3\ {\mathbf{PO}} . {\mathbf{OL}} / {D}^{2} \right)\\ \end{eqnarray*}$

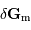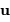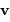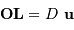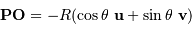On trouve alors pour le champ de marée $\delta \mathbf{G} _{\mathrm{m}}$ , en introduisant les vecteurs unitaires $\mathbf{u}$ et $\mathbf{v}$ tels que ${\mathbf{OL}} = D\ \mathbf{u}$ et ${\mathbf{PO}} = -R (\cos\theta\ \mathbf{u} + \sin\theta\ \mathbf{v})$ :

$\begin{eqnarray*} \delta \mathbf{G} _{\mathrm{m}} &=& {{\cal G} m} \left[ { {\mathbf{PO}} \over {D}^{3}} - {3\ {\mathbf{PO}} . {\mathbf{OL}} \over {D}^{2}}\ { {\mathbf{OL}} \over {D}^{3}} \right]\\ &=& {{\cal G} m\over {D}^{3}} \left[-R\ (\cos\theta\ \mathbf{u} + \sin\theta\ \mathbf{v}) + 3 R\ \cos\theta\ \mathbf{u} \right]\\ &=& {{\cal G} m R\over {D}^{3}} \left[2 \cos \theta\ \mathbf{u} - \sin \theta\ \mathbf{v} \right]\\ \end{eqnarray*}$

On peut comparer les modules des champs de marée et gravitationnel :

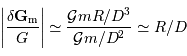
$\left\vert { \delta \mathbf{G} _{\mathrm{m}}\over G}\right\vert \simeq {{\cal G}mR/D^3\over {\cal G}m/D^2} \simeq R/D$

Il ressort de cette analyse que l'effet de marée :