| La gravité comme force à distance | Les forces électromagnétiques | Nature de la gravité | Les ondes gravitationnelles : propagation | Ondes gravitationnelles : génération | Les ondes gravitationnelles : détection |
La métrique |
Nous avons écrit que la présence de matière modifie la géométrie de l'espace. En fait, la propriété modifiée est la métrique, c'est-à-dire la loi qui donne la distance entre deux points.
Pour comprendre qu'est-ce que l'on entend par la loi qui donne la distance entre deux points, commencons par le cas simple de deux points de coordonnées 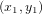 et
et 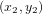 sur le plan cartésien (Fig. 1a). La distance dl entre les deux points est donnée par le théorème de Pythagore :
sur le plan cartésien (Fig. 1a). La distance dl entre les deux points est donnée par le théorème de Pythagore :
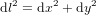 (1),
(1),
où 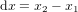 et
et 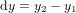 .
.
Nous pouvons généraliser l'équation (1) au cas de deux points 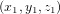 et
et 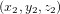 dans l'espace en troi dimensions. En appliquant deux fois le théorème de Pythagore (Fig. 1b), nous trouvons :
dans l'espace en troi dimensions. En appliquant deux fois le théorème de Pythagore (Fig. 1b), nous trouvons :
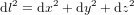 (2).
(2).
Les équations (1) et (2) expriment la métrique euclienne, respectivement en deux et trois dimensions. La métrique euclidienne est la loi qui permet de calculer la distance dl entre deux points n'importe quels dans la géométrie d'Euclide.
Les équations (1) et (2) sont formulées en coordonnées cartésiennes orthogonales. On aurait pu considérer d'autres systèmes de coordonnées, par exemple, en deux dimensions, les coordonnées polaires. En coordonnées polaires (Fig. 2a), un point P est identifié par deux coordonnées : la distance r de l'origine O et l'angle  que la droite OP forme avec une droite de référence. Dans ce système de coordonnées, la distance
que la droite OP forme avec une droite de référence. Dans ce système de coordonnées, la distance 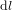 entre les points
entre les points 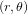 et
et 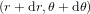 est déterminée par l'équation :
est déterminée par l'équation :
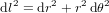 (3),
(3),
qui exprime, encore une fois, le théorème de Pythagore, cette fois en coordonnées polaires.
Cépendant, un changement de coordonnées n'est pas un changement de métrique. Les équations (1) et (3) ont des formes différentes, mais elles correspondent à la même métrique parce qu'elles donnent le même résultat pour la distance 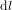 entre deux points*. Un changement de métrique est – nous verrons bientôt – quelque chose de plus profond.
entre deux points*. Un changement de métrique est – nous verrons bientôt – quelque chose de plus profond.
*Affirmer que les équations (1) et (3) donnent le même résultat pour la longeuer 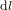 est correct dans la limite que
est correct dans la limite que 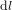 est infinitésimale. Autrement, on ne peut pas traiter l'arc de cercle de longeuer
est infinitésimale. Autrement, on ne peut pas traiter l'arc de cercle de longeuer 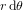 comme un segmant et l'on ne peut pas supposer qu'il soit perpendiculaire au segment de longeure
comme un segmant et l'on ne peut pas supposer qu'il soit perpendiculaire au segment de longeure 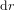 .
.
Pour comprendre comment la métrique peut différer de celle d'Euclide, considérons la géométrie sur une surface sphérique (par exemple, le globe terrestre; Fig. 2b).
Un lieu sur le globe est identifié par deux coordonnées : la latitude  et la longitude
et la longitude 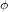 , étant donné que la distance r du centre de la Terre est la même pour tous les points. A
, étant donné que la distance r du centre de la Terre est la même pour tous les points. A 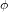 , constante, une variation infinitésimale
, constante, une variation infinitésimale 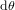 de la latitude correspond à un déplacement de
de la latitude correspond à un déplacement de 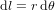 , si les angles sont exprimés en radians. A
, si les angles sont exprimés en radians. A  constante, une variation infinitésimale
constante, une variation infinitésimale 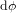 de la longitude correspond à un déplacement de
de la longitude correspond à un déplacement de 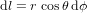 . Dans la limite que des arcs infinitésimaux peuvent être considérés rectilignes, le théorème de Pythagore donne :
. Dans la limite que des arcs infinitésimaux peuvent être considérés rectilignes, le théorème de Pythagore donne :
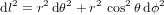 (4).
(4).
L'équation (4) est fondamentalement différentes des équations (1) et (3). Les équations (1) et (3) donnent la distance entre deux points sur le plan, donc une surface platte. L'équation (4) donne l'élément infinitésimal de distance sur une sphère, donc une surface courbe.
Pour mieux comprendre cette différence, considérons la distance l entre le pôle Nord et le pôle Sud de la Terre : l est le diamètre terrestre si on voit les pôles comme deux points dans l'espace en trois dimensions et le méridien terrestre si on voit les pôles comme deux points sur la surface terrestre. La métrique (2) correspond au premier cas, 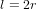 . La métrique (4) correspond au deuxième cas,
. La métrique (4) correspond au deuxième cas, 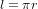 . La métrique (4) est non-euclidienne parce qu'elle mesuren les distances sur une surface courbe.
. La métrique (4) est non-euclidienne parce qu'elle mesuren les distances sur une surface courbe.
Pour résumer, l'équation (1) donne la métrique sur une surface platte. L'équation (2) donne la métrique dans un espace plat (en espace qui obéit à la géométrie d'Euclide). La notion de distance sur une surface peut être généralisée à des surfaces courbes. C'est comme ça que l'on passe de la métrique (1) à la métrique (4). De ma même manière, la notion de distance dans l'espace en troi dimensions (équation 2) peut être généralisée à des espaces courbes, qui correspondent à des métriques plus complexes et n'obéissent pas à la géométrie d'Euclide.
Pour un système de coordonnées n'importe lesquelles, la distance spatiale 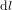 entre le point de coordonnées
entre le point de coordonnées 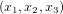 et le point de coordonnées
et le point de coordonnées 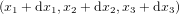 est donnée par la formule :
est donnée par la formule :
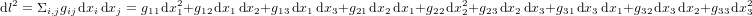 (5).
(5).
La matrice 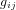 en équation (5) définit la métrique. Dans un système de coordonnées cartesiennes orthogonales,
en équation (5) définit la métrique. Dans un système de coordonnées cartesiennes orthogonales, 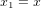 ,
, 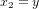 et
et 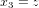 . Dans ce système de coordonnées, la métrique euclidienne prend la forme très simple
. Dans ce système de coordonnées, la métrique euclidienne prend la forme très simple 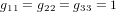 et
et 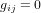 pour
pour 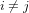 .
.
Dans d’autres géométries ou d'autres systèmes de coordonnées, la métrique prend des formes plus compliquées. Heureusement, on peut toujours trouver un système de coordonnées astucieux dans lequel les termes 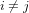 disparaissent localement. On peut démontrer que cette propriété suit de la symétrie de la métrique, c'est-à-dire du fait que la distance entre A et B doit être égale à la distance entre B et A. Pour cette raison, nous ne considérerons des métriques de la forme (dite diagonale) :
disparaissent localement. On peut démontrer que cette propriété suit de la symétrie de la métrique, c'est-à-dire du fait que la distance entre A et B doit être égale à la distance entre B et A. Pour cette raison, nous ne considérerons des métriques de la forme (dite diagonale) :
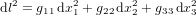 (6).
(6).
Des formes plus complexes sont rarement considérées, même dans les cours de maîtrise.
En coordonnées sphériques (Fig. 2b), 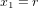 ,
, 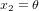 et
et 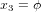 . Nous laissons au lecteur l'exercice de calculer les valeurs des coéfficients
. Nous laissons au lecteur l'exercice de calculer les valeurs des coéfficients 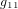 ,
, 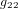 ,
, 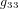 pour la métrique euclidienne dans un tel système de coordonnées.
pour la métrique euclidienne dans un tel système de coordonnées.